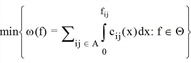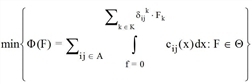Das Verkehrsnetz wird durch einen gerichteten Graphen repräsentiert G = (N, A), wobei N die Menge aller Knoten ist und A ⊆ NxN die Menge aller Kanten. Die Graph-Knoten repräsentieren Bezirksschwerpunkte und Straßenkreuzungen ( Visum-Netzknoten), die Kanten Strecken und Anbindungen. Werden Abbieger mit Widerstand oder Einschränkungen ins Netzmodell eingefügt, wird der Knoten aufgelöst, damit solche Abbieger bestimmten oder keinen Kanten des Graphen zugeordnet werden.
Folgende Notation wird verwendet:
|
fij |
Gesamtbelastung auf Kante ij∈A, Element des (|A|x1) Vektors f |
|
cij |
Kosten der Kante ij∈A, Element des (|A|x1) Vektors c |
|
cij(fij) |
Kostenfunktion der Kante ij∈A |
|
Z ⊆ N |
Menge der Bezirksschwerpunkte |
|
Dod |
Nachfrage zwischen Quelle o∈Z und Ziel d∈Z, Element des (|Z|2x1) Vektors D, d.h. der zeilenweise angeordneten Nachfragematrix |
|
Kid |
Menge der azyklischen Wege zwischen Knoten i∈N und Ziel d∈Z |
|
K |
K = ∪o∈Z∪d∈ZKod ist die Menge der Wege, die dem Verkehrsteilnehmer zur Verfügung stehen |
|
δijk |
δijk = 1, wenn Kante ij∈A zu Weg k gehört, und 0, andernfalls – für k∈K, ist dies ein Element der (|A|x|K|) Matrix ∆ |
|
λodk |
λodk ist 1, wenn Weg k∈K die Quelle o∈Z mit dem Ziel d∈Z (d.h. k∈Kod) verbindet, und andernfalls 0, Element der (|Z|2x|K|) Matrix Λ |
|
Fk |
Belastung auf Weg k∈K, Element des (|K|x1) Vektors F |
|
Ck |
Kosten des Weges k – für k∈K ist dies Element des (|K|x1) Vektors C |
|
Wid |
minimale Kosten zur Erreichung des Ziels d∈Z von Knoten i∈N |
|
ℜ |
Menge der reellen Zahlen |
|
|S| |
Kardinalität der generischen Menge S |
Es gibt zwei fundamentale Beziehungen zwischen Belastungsvariablen. Die Belastung auf Kante ij∈A ist die Summe der Belastungen auf den Wegen, die die Kante überfahren:
fij = ∑k∈Kδijk • Fk
Die Verkehrsnachfrage zwischen der Quelle o∈Z und dem Ziel d∈Z muss übereinstimmen mit der Summe der Belastungen auf den Wegen, die diese verbinden:
∑k∈KodFk = Dod
Außerdem müssen alle Wegbelastungen die Nicht-Negativitäts-Bedingungen erfüllen.
Wie gewöhnlich werden additive Wegekosten vorausgesetzt, d.h. der Widerstand Ck, den Nutzer einem gegebenen Weg k zuordnen, ist die Summe der Kosten auf den Kanten, die zu ihm gehören:
Ck = ∑ij∈Aδijk • cij [6]
Definitionsgemäß sind die minimalen Kosten zum Erreichen von Ziel d∈Z von Knoten i∈N die Kosten jedes Kurzwegs, der sie verbindet:
Wid = min{Ck : k∈Kid} [7]
In diesem Fall kann das Umlegungsproblem durch folgendes Programm formalisiert werden:
wobei
|
Θ |
{f∈ℜ|A|: f = ∆•F, F∈Ω} die Menge der zulässigen Kantenbelastungen |
|
Ω |
{F∈ℜ|K|: F≥ 0, Λ • F = D} die Menge der zulässigen Wegbelastungen |
QUm die Existenz und Eindeutigkeit der Lösung von Problem [8] sicherzustellen, gehen wir davon aus, dass:
cij(fij) nicht-negativ, kontinuierlich, streng monoton steigend ist;
Kod nicht-leer ist;
Dod nicht-negativ ist.
Das konvexe Problem [8] kann in Bezug auf Wegbelastungen auch wie folgt ausgedrückt werden:
wobei die Konvexität des mathematischen Programms bewahrt wird, obwohl die Lösungseindeutigkeit nicht länger gewährleistet ist, was bedeutet, dass jeder absteigende Algorithmus innerhalb von Wegbelastungen eine globale Lösung liefert, die dann eine konvexe Menge darstellt.
Die Relevanz der Gleichung [9] für Verkehrsumlegungen liegt darin begründet, dass sich im Fall von additiven Wegekosten, die (notwendigen) Bedingungen erster Ordnung mit folgender Formulierung des deterministischen Nutzergleichgewichts auf der Basis des Wardrop-Prinzips für jedes o∈Z und d∈Z decken:
Fk • (Ck - Wod) = 0, ∀k∈Kod [10.1]
Ck ≥ Wod, ∀k∈Kod [10.2]
Fk ≥ 0, ∀k∈Kod [10.3]
Auf der Basis von [10.1] bis [10.4]
- haben alle genutzten Wege (Fk > 0) die minimalen Kosten (Ck = Wod);
- hat jeder nicht genutzte Weg (Fk = 0) keine niedrigeren Kosten (Ck≥Wod).
Ein Nutzergleichgewicht liegt vor, wenn die Bedingungen [10.1] bis [10.4] gleichzeitig für jede Quelle-Ziel-Beziehung gelten, wobei angenommen wird, dass jeder Wegkostenwert Ck eine Funktion (potenziell) aller Wegbelastungen F ist, aufgrund der Kantenkostenfunktion:
Ck = ∑ij∈Aδijk • cij(∑k∈Kδijk • Fk), in kompakter Form C = ΔT • c(Δ•F) [11]
Da der Gradient von Φ (F)C = ΔT • c(Δ•F) ist, erhalten wir für X→F durch die Linearisierung der Zielfunktion von Problem [9] an einem Punkt F∈Ω:
Φ(X) = Φ(F) + CT•(X-F) + o(||X-F||). [12]
Aus Gleichung [12] erkennen wir, dass eine Richtung E-F genau dann fallend ist, wenn:
Um also die Zielfunktion zu senken und die Zulässigkeit zu erhalten, müssen zwangsläufig Wegbelastungen so verschoben werden, dass deren Gesamtkosten hinsichtlich des aktuellen Kostenprofils niedriger werden, d.h. die aktuelle Lösung wird von F zu einem E∈Ω verschoben, sodass CT•E < CT•F, wobei C = ΔT•c(Δ•F). Die Notwendigkeit ergibt sich aus der Konvexität des Problems, da in diesem Fall an jedem Punkt X mit CT•(X-F) > 0 gilt: Φ(X) > Φ(F).
Diese Herangehensweise zur Ermittlung einer Abstiegsrichtung kann auf jede Quelle-Ziel-Beziehung einzeln, auf jedes Ziel, oder auf das gesamte Netz angewandt werden. Basierend auf der obigen allgemeinen Regel liefert das Setzen der Belastungen E mittels einer Alles-oder-Nichts-Umlegung auf Kurzwege eindeutig eine Abstiegsrichtung. Übernehmen wir solch eine Richtung für alle QZ-Beziehungen gleichzeitig und wenden gleichzeitig eine Liniensuche an, erhalten wir den bekannten Frank-Wolfe-Algorithmus. Im Gleichgewicht verwendet jede QZ-Beziehung jedoch typischerweise mehrere Wege, was bedeutet, dass jede Abstiegsrichtung, die einen einzelnen Weg belastet, eigentlich kurzsichtig ist; tatsächlich konvergieren solche Algorithmen nur langsam.
Sobald eine zulässige Abstiegsrichtung E-F bekannt ist, können wir, da Ω konvex ist, die aktuelle Lösung entlang dem Segment F+α•(E-F) bewegen und einen Schritt α∈(0,1] durchführen, damit die Zielfunktion von Problem [9], geschrieben als Φ(α) = Φ(F+α•(E-F)), ausreichend gesenkt wird. Da Φ sowohl C1 als auch konvex ist, und somit auch Φ, sind mehrere Methoden verfügbar, um ein α zu bestimmen, das Φ(α) minimiert. Visum verwendet eine Armijo-ähnliche Suche und ermittelt den größten Schritt α = 0.5k für alle nicht-negativen Ganzzahlen k, sodass
∂ Φ(0.5k)/∂α < 0. [14]
Bei dieser Methode muss die gerichtete Ableitung der Zielfunktion berechnet werden:
∂Φ(α)/∂α = [c(Δ•(F+α•(E-F)))]T•[Δ•(E-F)], [15]
was voraussetzt, dass die Kantenkosten an den Kandidatenbelastungen F+α•(E-F) ausgewertet werden und dann die Differenz zwischen den zugehörigen Gesamtkosten, die aus den Belastungen E und F ermittelt wurden. Sind solche Gesamtkosten mit E kleiner als solche mit F, dann ist ∂Φ(α)/α negativ, sodass die optimale Lösung mehr in Richtung E geht, und umgekehrt.